Casa
four square theorem

Euler Four-Square Identity -- from Wolfram MathWorld

Por um escritor misterioso

Descrição
The amazing polynomial identity communicated by Euler in a letter to Goldbach on April 12, 1749 (incorrectly given as April 15, 1705--before Euler was born--in Conway and Guy 1996, p. 232). The identity also follows from the fact that the norm of the product of two quaternions is the product of the norms (Conway and Guy 1996).
Euler Four-Square Identity -- from Wolfram MathWorld
Intensity Constraint Gradient-Based Image Reconstruction
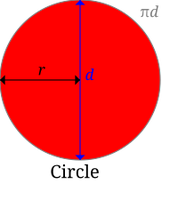
Euler Four-Square Identity -- from Wolfram MathWorld
Pi, Number in Math Wiki
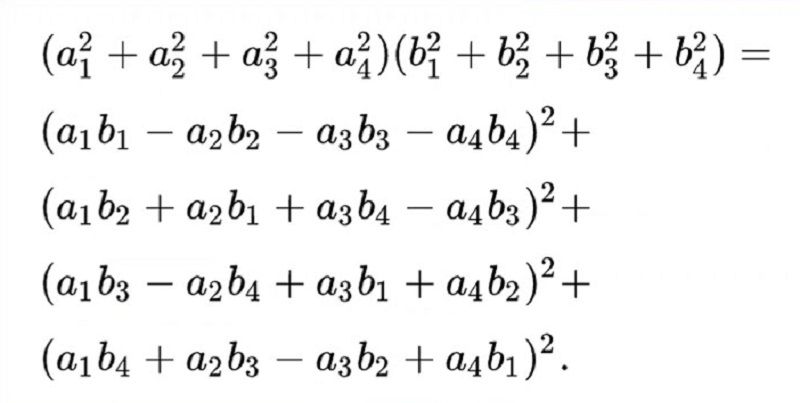
Euler Four-Square Identity -- from Wolfram MathWorld
Leonhard Euler's Contributions in Mathematics – StudiousGuy
Euler Four-Square Identity -- from Wolfram MathWorld
These two equations are equivalent but Desmos and Geogrbra both
Euler Four-Square Identity -- from Wolfram MathWorld
Euler's four-square identity - Wikipedia
Euler Four-Square Identity -- from Wolfram MathWorld
Maths Ed Ideas: On Descartes Numbers
Euler Four-Square Identity -- from Wolfram MathWorld
Euler Angles -- from Wolfram MathWorld
Euler Four-Square Identity -- from Wolfram MathWorld
PDF) Taylor's series expansions for real powers of two functions
Euler Four-Square Identity -- from Wolfram MathWorld
Magic square - Wikipedia
Euler Four-Square Identity -- from Wolfram MathWorld
Open problem in number theory
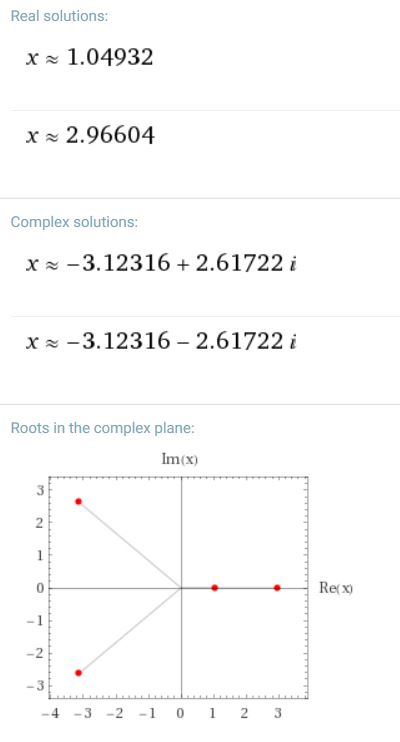
Euler Four-Square Identity -- from Wolfram MathWorld
mathematics Archives - The Billy Lee Pontificator
Euler Four-Square Identity -- from Wolfram MathWorld
Maths Ed Ideas: Curriculum Stories: The Absurd Equation
Euler Four-Square Identity -- from Wolfram MathWorld
The Most Striking Equation in Mathematics – Galileo's Pendulum
Euler Four-Square Identity -- from Wolfram MathWorld
Prove that Euler's four-square identity, Pfister's identity
de por adulto (o preço varia de acordo com o tamanho do grupo)